算法讲课---1、贪心
一、总结
一句话总结:贪心算法在解决问题的策略上“目光短浅”
一个贪心算法总是做出当前最好的选择,也就是说,它期望通过局部最优选择从而得到全局最优的解决方案。
1、贪心导入问题
有n堆苹果,每堆苹果苹果的个数不限(大于一个),要从这n堆苹果中每堆选取一个,使得所选的苹果的总重量最大,怎么求
2、导入问题求解
显然解决方法就是取每堆最重的那个就好,这里就用了贪心
3、导入问题的贪心思想具体分析
贪心解决问题的三个步骤为:
a、确定贪心策略
b、根据贪心策略,一步一步得到局部最优解
c、将局部最优解合并起来就得到全局最优解
导入问题中上述贪心的三个步骤的运用:
a、贪心策略:取每堆中最重的那个苹果
b、局部最优解:把每堆最重的那个苹果取出来
c、全局最优解:将取出来的所有苹果放到一起,就是我们要求的答案
4、贪心中注意的问题有哪些?
在贪心算法中,我们需要注意以下几个问题。
(1)没有后悔药。一旦做出选择,不可以反悔。
(2)有可能得到的不是最优解,而是最优解的近似解。
(3)选择什么样的贪心策略,直接决定算法的好坏。
5、贪心的本质和思想是什么?
一个贪心算法总是做出当前最好的选择,也就是说,它期望通过局部最优选择从而得到全局最优的解决方案。
贪心算法在解决问题的策略上“目光短浅”
6、什么样的问题能用贪心来求解?
利用贪心算法求解的问题往往具有两个重要的特性:贪心选择性质和最优子结构性质。
(1)贪心选择
所谓贪心选择性质是指原问题的整体最优解可以通过一系列局部最优的选择得到。(2)最优子结构
当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。
7、导入问题为什么适合用贪心来求解?
(1)贪心选择:所谓贪心选择性质是指原问题的整体最优解可以通过一系列局部最优的选择得到。
显然满足
(2)最优子结构:当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。
这里涉及到怎么把导入问题划分出子结构:
例如原问题S={a1,a2,…,ai,…,an},通过贪心选择选出一个当前最优解{ai}之后,转化为求解子问题S−{ai},如果原问题的最优解包含子问题的最优解,则说明该问题满足最优子结构性质
贪心选择:b和c之间的那条链
最优子结构:问题能分成子问题
a、贪心策略:
b、局部最优解:
c、全局最优解:
8、一般的问题如何划分出子问题(比如求每堆苹果最大的问题)?
例如原问题S={a1,a2,…,ai,…,an},通过贪心选择选出一个当前最优解{ai}之后,转化为求解子问题S−{ai},如果原问题的最优解包含子问题的最优解,则说明该问题满足最优子结构性质
a、取了第一堆的最重苹果,剩下的问题就变成了一个子问题
b、每一堆可以看成一个子问题
9、什么问题不能用贪心来求解?
哪些用dp来求解的问题一般都不能用贪心
10、利用贪心求解的经典算法实例有哪些?
a、最优装载问题
有一天,海盗们截获了一艘装满各种各样古董的货船,每一件古董都价值连城,一旦打碎就失去了它的价值。虽然海盗船足够大,但载重量为C,每件古董的重量为wi,海盗们该如何把尽可能多数量的宝贝装上海盗船呢?
贪心策略:依次取重量最小的古董
b、背包问题
假设山洞中有 n 种宝物,每种宝物有一定重量w 和相应的价值v,毛驴运载能力有限,只能运走m 重量的宝物,一种宝物只能拿一样,宝物可以分割。那么怎么才能使毛驴运走宝物的价值最大呢?我们可以尝试贪心策略:(1)每次挑选价值最大的宝物装入背包,得到的结果是否最优?(2)每次挑选重量最小的宝物装入,能否得到最优解?(3)每次选取单位重量价值最大的宝物,能否使价值最高?
c、会议安排问题

d、最短路径(Dijkstra)


e、哈夫曼编码
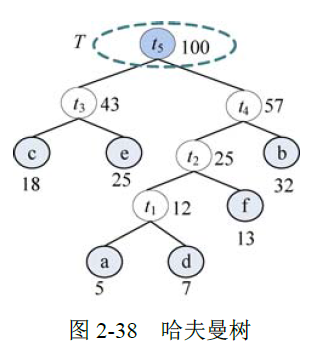
f、最小生成树(prim算法)
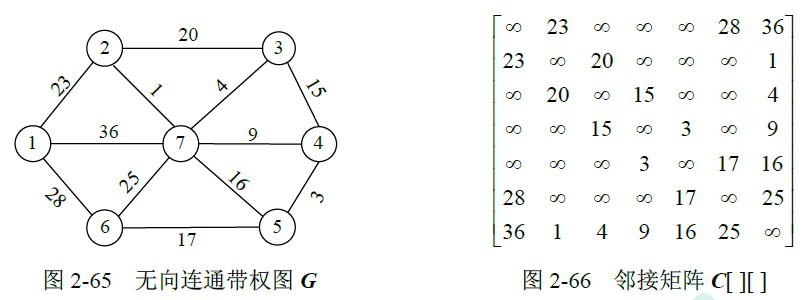
11、贪心和动态规划的区别是什么?
动态规划算法通常以自底向上的方式解各子问题,是递归过程。
贪心算法则通常以自顶向下的方式进行,以迭代的方式作出相继的贪心选择,每作一次贪心选择就将所求问题简化为规模更小的子问题。
以二叉树遍历为例:
贪心法是从上到下仅仅进行深度搜索。也就是说它从根节点一口气走到黑的,它的代价取决于子问题的数目,也就是树的高度,每次在当前问题的状态上作出的选择都是1。不进行广度搜索。所以终于它得出的解不一定是最优解。非常有可能是近似最优解。
而动态规划法在最优子结构的前提下,从树的叶子节点開始向上进行搜索,而且在每一步都依据叶子节点的当前问题的状况作出选择,从而作出最优决策。所以她的代价是子问题的个数和可选择的数目。它求出的解一定是最优解。
12、背包问题和0/1背包的区别是什么?
物品可分割的装载问题我们称为背包问题,物品不可分割的装载问题我们称之为0-1 背包问题。
13、怎么判断贪心策略的正误?
比如:会议安排问题

举特例:
比如第一种贪心策略就可以举一个最早开始但是持续时间是10000个小时的特例来判断错误
比如第二种贪心策略就可以举一个20时才开始持续一个小时的特例(这个特例不好,就是时间很小的很稀少很分散的时候可以判断贪心策略二是错误的)
14、子问题是什么?
问题和原问题一样,只是规模变小了
比如规模从n->1
或者规模从n->n-1
15、有n堆苹果,每堆苹果苹果的个数不限(大于一个),要从这n堆苹果中每堆选取一个,使得所选的苹果的总重量最大,的两种子问题划分方式是什么?
a、规模从n->1,分成n堆取最大
b、规模从n->n-1,取了最大的那个,那堆不能取了,从剩下的n-1堆中每堆取一个使所选苹果的总重量最大
二、五大算法思想—贪心算法
怎么理解
贪心法在解决这个问题的策略上目光短浅,仅仅依据当前已有的信息就做出选择,并且一旦做出了选择。无论将来有什么结果,这个选择都不会改变。
一句话:不求最优,仅仅求可行解。
怎样推断
对于一个详细的问题,怎么知道是否可用贪心算法解此问题,以及是否能得到问题的最优解?
我们能够依据贪心法的2个重要的性质去证明:贪心选择性质和最优子结构性质。
1、贪心选择
什么叫贪心选择?从字义上就是贪心也就是目光短线。贪图眼前利益。在算法中就是仅仅依据当前已有的信息就做出选择,并且以后都不会改变这次选择。(这是和动态规划法的主要差别)
所以对于一个详细问题。要确定它是否具有贪心选择性质,必须证明每做一步贪心选择是否终于导致问题的总体最优解。
2、最优子结构
当一个问题的最优解包括其子问题的最优解时,称此问题具有最优子结构性质。
这个性质和动态规划法的一样,最优子结构性质是可用动态规划算法或贪心算法求解的关键特征。
区分动态规划
动态规划算法通常以自底向上的方式解各子问题,是递归过程。
贪心算法则通常以自顶向下的方式进行,以迭代的方式作出相继的贪心选择,每作一次贪心选择就将所求问题简化为规模更小的子问题。
以二叉树遍历为例:
贪心法是从上到下仅仅进行深度搜索。也就是说它从根节点一口气走到黑的,它的代价取决于子问题的数目,也就是树的高度,每次在当前问题的状态上作出的选择都是1。不进行广度搜索。所以终于它得出的解不一定是最优解。非常有可能是近似最优解。
而动态规划法在最优子结构的前提下,从树的叶子节点開始向上进行搜索,而且在每一步都依据叶子节点的当前问题的状况作出选择,从而作出最优决策。所以她的代价是子问题的个数和可选择的数目。它求出的解一定是最优解。
一般求解过程
使用贪心法求解能够依据下面几个方面进行(终于也相应着每步代码的实现),以找零钱为例:
1、候选集合(C)
通过一个候选集合C作为问题的可能解。(终于解均取自于候选集合C)
比如。在找零钱问题中,各种面值的货币构成候选集合。
2、解集合(S)
每完毕一次贪心选择,将一个解放入S。终于获得一个完整解S
3、解决函数(solution)
检查解集合S是否构成问题的完整解。
比如,在找零钱问题中。解决函数是已付出的货币金额恰好等于应付款。
4、选择函数(select)
即贪心策略。这是贪心法的关键,选择出最有希望构成问题的解的对象。
(这个选择函数通常和目标函数有关)
比如,在找零钱问题中,贪心策略就是在候选集合中选择面值最大的货币。
5、可行函数(feasible)
检查解集合中增加一个候选对象是否可行。(增加下一个对象后是不是满足约束条件)
比如。在找零钱问题中,可行函数是每一步选择的货币和已付出的货币相加不超过应付款。
C的实现:(一般试题就是在这个基础上加入详细的实现)
Greedy(C) //C是问题的输入集合即候选集合{ S={ }; //初始解集合为空集 while (not solution(S)) //集合S没有构成问题的一个解 { x=select(C); //在候选集合C中做贪心选择 if feasible(S, x) //推断集合S中增加x后的解是否可行 S=S+{x}; C=C-{x}; } return S;} 小结
像找零问题,背包问题。近期临点都是非常经典的贪心算法。并且都是实际的问题。理解上不太难,对于算法题,在理解算法思想的基础上,多做题,查找规律,多总结一些C实现中重要的代码段。
参考: 五大算法思想—贪心算法 - gavanwanggw - 博客园
https://www.cnblogs.com/gavanwanggw/p/7141358.html
三、贪心算法经典例子
一、定义
什么是贪心算法呢?所谓贪心算法是指,在对问题求解时,总是做出在当前看来最好的选择。也就是说,不从整体最优解出发来考虑,它所做出的仅是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解,但对范围相当广泛的许多问题都能产生整体最优解或整体最优解的近似解。 贪心算法的基本思路如下: 1.建立数学模型来描述问题。 2.把求解的问题分成若干个子问题。 3.对每个子问题求解,得到每个子问题的局部最优解。 4.把每个子问题的局部最优解合成为原来问题的一个解。 实现该算法的过程: 从问题的某一初始状态出发; while 能朝给定总目标前进一步 do 求出可行解的一个解元素; 由所有解元素组合成问题的一个可行解;
二、例题分析
[活动安排问题] 活动安排问题是可以用贪心算法有效求解的一个很好的例子。该问题要求高效地安排一系列争用某一公共资源的活动。贪心算法提供了一个简单、漂亮的方法使得尽可能多的活动能兼容地使用公共资源。
设有n个活动的集合e={1,2,…,n},其中每个活动都要求使用同一资源,如演讲会场等,而在同一时间内只有一个活动能使用这一资源。每个活动i都有一个要求使用该资源的起始时间si和一个结束时间fi,且si< fi。如果选择了活动i,则它在半开时间区间[si,fi]内占用资源。若区间[si,fi]与区间[sj,fj]不相交,则称活动i与活动j是相容的。也就是说,当si≥fi或sj≥fj时,活动i与活动j相容。活动安排问题就是要在所给的活动集合中选出最大的相容活动子集合。
在下面所给出的解活动安排问题的贪心算法gpeedyselector中,各活动的起始时间和结束时间存储于数组s和f{中且按结束时间的非减序:.f1≤f2≤…≤fn排列。如果所给出的活动未按此序排列,我们可以用o(nlogn)的时间将它重排。
/** * 活动时间安排 */@Testpublic void testArrangeActivity() { int[] start = { 1, 3, 0, 5, 3, 5, 6, 8, 8, 2, 12}; int[] end = { 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}; List results = arrangeActivity(start, end); for (int i = 0; i < results.size(); i++) { int index = results.get(i); System.out.println("开始时间:" + start[index] + ",结束时间:" + end[index]); }}/** * 活动安排 * * @param s 开始时间 * @param e 结束时间 * @return */public List arrangeActivity(int[] s, int[] e) { int total = s.length; int endFlag = e[0]; List results = new ArrayList<>(); results.add(0); for (int i = 0; i < total; i++) { if (s[i] > endFlag) { results.add(i); endFlag = e[i]; } } return results;}
[找零钱问题]假如老板要找给我99分钱,他有上面的面值分别为25,10,5,1的硬币数,为了找给我最少的硬币数,那么他是不是该这样找呢,先看看该找多少个25分的,诶99/25=3,好像是3个,要是4个的话,我们还得再给老板一个1分的,我不干,那么老板只能给我3个25分的拉,由于还少给我24,所以还得给我2个10分的和4个1分。
@Testpublic void testGiveMoney() { //找零钱 int[] m = { 25, 10, 5, 1}; int target = 99; int[] results = giveMoney(m, target); System.out.println(target + "的找钱方案:"); for (int i = 0; i < results.length; i++) { System.out.println(results[i] + "枚" + m[i] + "面值"); }}public int[] giveMoney(int[] m, int target) { int k = m.length; int[] num = new int[k]; for (int i = 0; i < k; i++) { num[i] = target / m[i]; target = target % m[i]; } return num;}
[背包问题]有一个背包,背包容量是M=150。有7个物品,物品可以分割成任意大小。
要求尽可能让装入背包中的物品总价值最大,但不能超过总容量。 物品 A B C D E F G 重量 35 30 60 50 40 10 25 价值 10 40 30 50 35 40 30 记得当时学算法的时候,就是这个例子,可以说很经典。 分析: 目标函数: ∑pi最大 约束条件是装入的物品总重量不超过背包容量,即∑wi<=M( M=150) (1)根据贪心的策略,每次挑选价值最大的物品装入背包,得到的结果是否最优? (2)每次挑选所占重量最小的物品装入是否能得到最优解? (3)每次选取单位重量价值最大的物品,成为解本题的策略? 贪心算法是很常见的算法之一,这是由于它简单易行,构造贪心策略简单。但是,它需要证明后才能真正运用到题目的算法中。一般来说,贪心算法的证明围绕着整个问题的最优解一定由在贪心策略中存在的子问题的最优解得来的。 对于本例题中的3种贪心策略,都无法成立,即无法被证明,解释如下: (1)贪心策略:选取价值最大者。反例: W=30 物品:A B C 重量:28 12 12 价值:30 20 20 根据策略,首先选取物品A,接下来就无法再选取了,可是,选取B、C则更好。 (2)贪心策略:选取重量最小。它的反例与第一种策略的反例差不多。 (3)贪心策略:选取单位重量价值最大的物品。反例: W=30 物品:A B C 重量:28 20 10 价值:28 20 10 根据策略,三种物品单位重量价值一样,程序无法依据现有策略作出判断,如果选择A,则答案错误。 值得注意的是,贪心算法并不是完全不可以使用,贪心策略一旦经过证明成立后,它就是一种高效的算法。比如,求最小生成树的Prim算法和Kruskal算法都是漂亮的贪心算法。
[均分纸牌]有N堆纸牌,编号分别为1,2,…,n。每堆上有若干张,但纸牌总数必为n的倍数.可以在任一堆上取若干张纸牌,然后移动。移牌的规则为:在编号为1上取的纸牌,只能移到编号为2的堆上;在编号为n的堆上取的纸牌,只能移到编号为n-1的堆上;其他堆上取的纸牌,可以移到相邻左边或右边的堆上。现在要求找出一种移动方法,用最少的移动次数使每堆上纸牌数都一样多。例如:n=4,4堆纸牌分别为:① 9 ② 8 ③ 17 ④ 6 移动三次可以达到目的:从③取4张牌放到④ 再从③区3张放到②然后从②去1张放到①。
输入输出样例:4 9 8 17 6 屏幕显示:3 算法分析:设a[i]为第I堆纸牌的张数(0<=I<=n),v为均分后每堆纸牌的张数,s为最小移动次数。 我们用贪心算法,按照从左到右的顺序移动纸牌。如第I堆的纸牌数不等于平均值,则移动一次(即s加1),分两种情况移动: 1.若a[i]>v,则将a[i]-v张从第I堆移动到第I+1堆; 2.若a[i]< v,则将v-a[i]张从第I+1堆移动到第I堆。为了设计的方便,我们把这两种情况统一看作是将a[i]-v从第I堆移动到第I+1堆,移动后有a[i]=v; a[I+1]=a[I+1]+a[i]-v. 在从第I+1堆取出纸牌补充第I堆的过程中可能回出现第I+1堆的纸牌小于零的情况。 如n=3,三堆指派数为1 2 27 ,这时v=10,为了使第一堆为10,要从第二堆移9张到第一堆,而第二堆只有2张可以移,这是不是意味着刚才使用贪心法是错误的呢? 我们继续按规则分析移牌过程,从第二堆移出9张到第一堆后,第一堆有10张,第二堆剩下-7张,在从第三堆移动17张到第二堆,刚好三堆纸牌都是10,最后结果是对的,我们在移动过程中,只是改变了移动的顺序,而移动次数不便,因此此题使用贪心法可行的。@Testpublic void testMoveCard() { //总共4堆 int heap = 4;// int[] cards = {9, 8, 17, 6}; int[] cards = { 10, 10, 20, 0}; int count = moveCards(cards, heap); System.out.println("移动次数:" + count); for (int i = 0; i < cards.length; i++) { System.out.println("第" + (i + 1) + "堆牌数:" + cards[i]); }}/** * 均分纸牌 * @param cards * @param heap * @return */public int moveCards(int[] cards, int heap) { //总牌数 int sum = 0; for (int i = 0; i < cards.length; i++) { sum += cards[i]; } //每堆平均牌数 int avg = sum / heap; //移动次数 int count = 0; for (int i = 0; i < cards.length; i++) { if(cards[i] != avg) { int moveCards = cards[i] - avg; cards[i] -= moveCards; cards[i + 1] += moveCards; count++; } } return count;} 利用贪心算法解题,需要解决两个问题:
一是问题是否适合用贪心法求解。我们看一个找币的例子,如果一个货币系统有三种币值,面值分别为一角、五分和一分,求最小找币数时,可以用贪心法求解;如果将这三种币值改为一角一分、五分和一分,就不能使用贪心法求解。用贪心法解题很方便,但它的适用范围很小,判断一个问题是否适合用贪心法求解,目前还没有一个通用的方法,在信息学竞赛中,需要凭个人的经验来判断。 二是确定了可以用贪心算法之后,如何选择一个贪心标准,才能保证得到问题的最优解。在选择贪心标准时,我们要对所选的贪心标准进行验证才能使用,不要被表面上看似正确的贪心标准所迷惑,如下面的例子。 [最大整数]设有n个正整数,将它们连接成一排,组成一个最大的多位整数。 例如:n=3时,3个整数13,312,343,连成的最大整数为34331213。 又如:n=4时,4个整数7,13,4,246,连成的最大整数为7424613。 输入:n N个数 输出:连成的多位数 算法分析:此题很容易想到使用贪心法,在考试时有很多同学把整数按从大到小的顺序连接起来,测试题目的例子也都符合,但最后测试的结果却不全对。按这种标准,我们很容易找到反例:12,121应该组成12121而非12112,那么是不是相互包含的时候就从小到大呢?也不一定,如12,123就是12312而非12123,这种情况就有很多种了。是不是此题不能用贪心法呢? 其实此题可以用贪心法来求解,只是刚才的标准不对,正确的标准是:先把整数转换成字符串,然后在比较a+b和b+a,如果a+b>=b+a,就把a排在b的前面,反之则把a排在b的后面。@Testpublic void testMaxNum() { //有n个正整数,将它们连接成一排,组成一个最大的多位整数 //12112错误 //12121正解// int[] nums = {12, 121}; int[] nums = { 12, 123}; String result = maxNum(nums); System.out.println("组成最大整数:" + result);}/** * 根据给定的整数组成最大的多位数 * @param nums */public String maxNum(int[] nums) { String result = ""; for (int i = 0; i < nums.length; i++) { String num1 = nums[i] + ""; for (int j = 1; j < nums.length; j++) { String num2 = nums[j] + ""; if ((num1 + num2).compareTo(num2 + num1) < 0) { int temp = nums[j]; nums[j] = nums[i]; nums[i] = temp; } } } for (int i = 0; i < nums.length; i++) { result += nums[i]; } return result;} 贪心算法所作的选择可以依赖于以往所作过的选择,但决不依赖于将来的选择,也不依赖于子问题的解,因此贪心算法与其他算法相比具有一定的速度优势。如果一个问题可以同时用几种方法解决,贪心算法应该是最好的选择之一。
参考